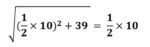Al-Khawarizmi adalah salah satu ilmuwan muslim yang sampai saat ini masih dihormati karena karyanya. Bahkan secara tidak sadar kita berhutang padanya, karena setiap hari kita telah menggunakan hasil buah karyanya yaitu algoritma. ia hidup pada masa Khalifah Al-Makmun dan merupakan seorang anggota di Baitul Hikmah.
Al-Khawarizmi dan Algebra
Orang-orang Eropa Timur mempelajari ajabar dari hasil karyanya. Istilah algebra dalam buku-buku latin merupakan adopsi dari judul asli bukunya yang berjudul“ Hisab al-Jabr wal Muqabbalah”. Mereka mengembangkannya hingga sampai saat ini tetap menjadi rujukan dalam matematika.
Secara keseluruhan menurut Jacques Sesiano– dalam bukunya yang berjudul “ An Introduction to the History of Algebra”—karya al-Khawarizmi berkaitan dengan perhitungan aljabar fundamental (bilangan, akar, kuadrat), solusi persamaan linier daan kuadratik, dasar-dasar perhitungan aljabar, dan selanjutnya pemecahan masalah sebanyak empat puluh.
Ia kemudian mengutip penjelasan al-Khawarizmi dalam buku Hisab al-Jabar wal Muqabbalah tentang buku tersebut yaitu,
“Sebuah karya pendek tentang aljabar, kaitannya dengan yang paling mudah dan berguna dalam aritmatika, seperti seorang laki-laki akan selalu membutuhkannya untuk urusan warisan, pembagian, tuntutan hukum, perdagangan, dan semua urusan mereka satu sama lain, seperti pengukuran tanah, penggalian kanal, perhitungan geometris, dan benda lainnya dari berbagai jenis”.
Aljabar dalam Sejarah
Kata aljabar dan muqabbalah sebelumnya tidak pernah ada di dalam khazanah matematika. Prof. Dr. Bartel Leenert van der Waerden dalam bukunya yang berjudul A History of Algebra From al-Khwarizmi to Emmy Noether menjelaskan bahwa Aljabar dimaknai dengan menambahkan bilangan yang sama pada kedua sisi sebuah persamaan agar menghilangkan bilangan negatif.
Atau dengan cara mengalikan kedua sisi sebuah persaaman dengan sebuah bilangan yang sama untuk menghilangan bentuk pecahan. Sedangkan Muqabbalah adalah mengurangi suku bilangan positif dengan jumlah yang sama dari kedua sisi persama. Bahasa umum yang lebih mudah adalah untuk menyamakan, menggabungkan atau menyelsaikan dengan lawan bilangan.
Kombinasi kata al-Jabar dan Muqabbalah ini kemudian di dunia modern dikenal secara lebih umum dengan penggunaan operasi aljabar, atau bisa juga disebut sebagai ilmu aljabar. Tetapi dalam karyanya, ia menyelesaikan persamalahan menggunakan kalimat retoris, dan tidak memiliki notasi. Ia memberikan contoh sebagaimana berikut :
“Saya telah membagi sepuluh menjadi dua bagian. Saya telah mengalikan salah satu dari dua bagian dengan yang lain. Setelah ini saya mengalikan salah satu dari keduanya dengan sendirinya, dan produk dari perkalian dengan sendirinya adalah empat kali lebih banyak dari salah satu bagian dengan yang lain.”
Kata “bagian” dalam contoh yang ditulis oleh al-Kawarizmi di atas adalah sesuatu yang dicari atau dalam bahasa matematisnya bisa diganti dengan variabel x atau variabel lainnya. Untuk menjelaskan lebih detail cara dia menyelesaikan soal tersebut, berikut saya turunkan uraian dari Rosen dalam bukunya yang berjudul “Algebra of Muhammed ben Musa”.
Menyelesaikan Soal Aljabar
Kata salah satu bagian itu dengan yang lainnya adalah minus sepuluh bagian, kemudian dia melipatgandakan keduanya, dan menguranginya dengan sepuluh bagian dikurangi kuadrat. Pada tulisan asli al-Khawarizmi nilai kuadrat dari bagian yang tidak diketahui ditulis dengan kata mal yang bisa berarti kekayaan. Sehingga didapatkan persamaan akhir yaitu “sebuah kuadrat sama dengan empat bagian dikurangi kuadrat”
Dalam notasi modern bisa dituliskan, x2 = 40x-4x2 kemudian penyelesaiannya menggunakan operasi aljabar yaitu menambahkan kedua sisi dengan 4x2 sehingga didapatkan:
x2 + 4x2 = 40x – 4x2 + 4x2
5x2= 40x atau x = 8
Sedangkan dalam contoh lainnya al-Khawarizmi menyelesaikan sebuah persamaan kuadrat dengan cara Muqabbalah, misal 50 + x2 = 29 + 10x
Cara muqabbalah adalah mengurangi dengan suku bilangan yang sama pada kedua sisi yaitu 29, sehingga persamaan kuadrat di atas menjadi
50 – 29 + x2 = 29 – 29 + 10x
21 + x2 = 10x
Kemudian al-Khawarizmi membuat enam persamaan yang sebenarnya tidak lain merupakan aturan tentang persamaan kuadrat. 1). ax2 = bx, 2). ax2 = c, 3). bx= c, 4). ax2 +bx = c, 5). ax2 +c = bx, 6). ax2 = bx+c. Enam persamaan tersebut sebenarnya dalam bentuk notasi modern.
Dalam tulisan asli al-Khawarizmi berbentuk kalimat retoris. Misal persamaan pertama adalah “persamaan kuadrat sama dengan akar”. Dan persamaan keempat adalah “persamaan kuadrat dan akar sama dengan bilangan”.
Contoh Penggunaan
Contoh penggunaanya sebagaimana diterjemahkan oleh Israel Kleiner dalam bukunya yang berjudul History of Algebra sebagaimana berikut:
“Apa yang menjadi kuadrat, yang ketika dijumlahkan sepuluh akarnya berjumlah tiga puluh sembilan dirham” ini maksudnya dalam symbol notasi modern adalah x2 + 10x= 39.
Solusinya adalah” Bagilah banyaknya akar menjadi dua bagian, yang mana menghasilkan lima. Nilai (lima) ini kalikan dengan dirinya sendiri, hasilnya adalah dua puluh lima. Tambahkan (dua puluh lima ini) pada tiga puluh sembilan, hasilnya adalah enam puluh empat. Sekarang, tariklah akar dari hasil ini (enam puluh empat), diperolehlah delapan.
Kemudian, delapan dikurangi setengah dari jumlah akar tadi (lima), diperoleh tiga. Inilah akar dari kuadrat yang Anda cari; kuadratnya sendiri adalah sembilan.”Dalam notasi modern persamaan kuadrat tersebut dapat dituliskan dalam bentuk symbol matematika yaitu akar dari (1/2 x 10)2 + 39 = 1/2 x 10
Meskipun dalam karyanya tersebut menggunakan kalimat retoris tanpa menggunakan simbol matematika modern, tetapi karyanya telah memberikan sumbangsih sangat besar dalam matematika. Tanpa karyanya mungkin tidak akan ada aljabar yang dituliskan dalam bentuk notasi dan simbol matematika modern yang dipelajari dengan mudah hingga kini.
Editor: Nabhan